936. Формулы Крамера
Решить систему
двух линейных уравнений с двумя неизвестными по формулам Крамера. Система
уравнений, приведенная во входных данных, имеет вид:
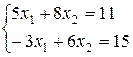
Вход. Первая строка содержит коэффициенты
первого уравнения, а вторая строка содержит коэффициенты второго. Все входные
числа разделены одним пробелом и не превышают 100 по модулю.
Выход. Первый
корень системы уравнений вывести в первой строке, а второй корень во второй
строке с точностью до 0.001.
|
Пример входа |
Пример выхода |
|
5 8
11 -3 6
15 |
-1.000 2.000 |
РЕШЕНИЕ
алгебра
- правило Крамера
Анализ алгоритма
Определителем называется число, равное
![]() = a * d – b * c
= a * d – b * c
Рассмотрим
систему уравнений:
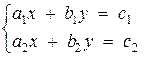
Помножим первое
уравнение на b2, а второе
на b1:
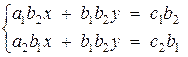
Вычтем из
первого уравнения второе:
(a1b2 – a2b1) x = c1b2 – c2b1
Или то же самое
что
 x =
x = 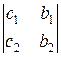
Аналогично в
исходной системе первое уравнение умножим на a2, а второе на a1:
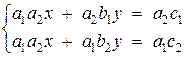
Вычтем из
второго уравнения первое:
(a1b2 – a2b1) y = a1c2 – a2c1
Или то же самое
что
 y =
y = 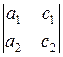
Обозначим
d =  , dx =
, dx = 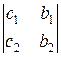 , dy =
, dy = 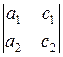
Тогда решение системы уравнений
можно записать в виде:
x = ![]() , y =
, y = ![]() , d ¹ 0
, d ¹ 0
Пример
Рассмотрим
систему уравнений 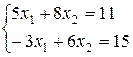 . Для нее имеем:
. Для нее имеем:
d =  = 5*6 + 3*8 = 54,
= 5*6 + 3*8 = 54,
dx =  = 11*6 – 15*8 = -54, dy =
= 11*6 – 15*8 = -54, dy =  = 5*15 + 3*11 = 108,
= 5*15 + 3*11 = 108,
откуда
x = -54 / 54 = -1, y
= 108 / 54 = 2
Реализация алгоритма
Функция kramer решает систему линейных уравнений
методом Крамера. Корни системы возвращаются в переменных x и y.
int
kramer(double a1, double
b1, double c1,
double a2, double
b2, double c2, double
&x, double &y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
При d = 0 прямые параллельны.
·
Если
dx = 0 (при этом будет и
dy
= 0), то прямые совпадают, возвращаем 2.
·
Если
dx ≠ 0 (при этом будет и
dy
≠ 0), то прямые не совпадают (не имеют общих точек), возвращаем
1.
if (d == 0) return (dx == 0.0) + 1;
При d ≠ 0 система имеет единственное решение,
которое вычисляем в паре (x, y). В
этом случае возвращаем 0.
x = dx / d; y = dy / d;
return 0;
}
Основная часть программы. Читаем
входные данные.
scanf("%lf %lf %lf",&a1,&b1,&c1);
scanf("%lf %lf %lf",&a2,&b2,&c2);
Решаем систему уравнений и выводим
ответ.
kramer(a1,b1,c1,a2,b2,c2,x,y);
printf("%.3lf\n%.3lf\n",x,y);
Java реализация
import java.util.*;
public class Main
{
static double[] kramer(double a1, double b1, double c1,
double a2, double b2, double c2)
{
double res[] = new double[3]; // type, x, y
double d = a1 * b2 - a2 * b1;
double dx = c1 * b2 - c2 * b1;
double dy = a1 * c2 - a2 * c1;
if (d == 0)
{
if (dx == dy && dx == 0.0) res[0] = 2;
else res[0] = 1;
}
else
{
res[1] = dx / d;
res[2] = dy / d;
res[0] = 0;
}
return res;
}
public static void
main(String []args)
{
Scanner con = new Scanner(System.in);
double a1 = con.nextDouble();
double b1 = con.nextDouble();
double c1 = con.nextDouble();
double a2 = con.nextDouble();
double b2 = con.nextDouble();
double c2 = con.nextDouble();
double res[] = kramer(a1,b1,c1,a2,b2,c2);
System.out.println(res[1] + "\n" + res[2]);
con.close();
}
}